C++で関数の近似(ニュートン補間)
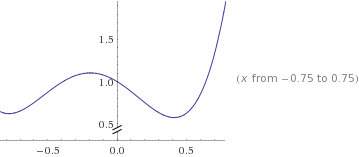
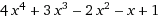
をニュートン補間で近似する
与えられた4個の関数値 f(x0), f(x1), f(x2), f(x3) を通る3次式を求める場合, まず次のような表を作る.

このとき,

と定義する.
これを x0とx1 の第1差分商, または1階差分商という.
同様に

と定義し, これを x0, x1, x2 の第2差分商, または2階差分商という.
第n差分商を

で表すと, 与えられた n+1点を通る n次式は次のように表すことができる.

この式を使って, 与えられた点以外の点の値を求める.
#include <iostream> #include <iomanip> #include <math.h> using namespace std; // データ点の数 const int N = 5; // 元の関数 double f(double x); // Newton (ニュートン) 補間 double newton(double d, double x[], double a[]); int main() { double x[N]; double y[N]; // 0.25刻みで -0.5〜0.5 まで, 5点だけ値をセット for (int i = 0; i < N; i++) { double d = i * 0.25 - 0.5; x[i] = d; y[i] = f(d); } // 差分商の表を作る double d[N][N]; //d[0][0] = y[0]; //d[0][1] = y[1]; //d[0][2] = y[2]; //d[0][3] = y[3]; //d[0][4] = y[4]; for (int j = 0; j < N; j++) d[0][j] = y[j]; //d[1][0] = (d[0][1] - d[0][0]) / (x[1] - x[0]); //d[1][1] = (d[0][2] - d[0][1]) / (x[2] - x[1]); //d[1][2] = (d[0][3] - d[0][2]) / (x[3] - x[2]); //d[1][3] = (d[0][4] - d[0][3]) / (x[4] - x[3]); //d[2][0] = (d[1][1] - d[1][0]) / (x[2] - x[0]); //d[2][1] = (d[1][2] - d[1][1]) / (x[3] - x[1]); //d[2][2] = (d[1][3] - d[1][2]) / (x[4] - x[2]); //d[3][0] = (d[2][1] - d[2][0]) / (x[3] - x[0]); //d[3][1] = (d[2][2] - d[2][1]) / (x[4] - x[1]); //d[4][0] = (d[3][1] - d[3][0]) / (x[4] - x[0]); for (int i = 1; i < N; i++) { for (int j = 0; j < N - i; j++) d[i][j] = (d[i-1][j+1] - d[i-1][j]) / (x[j+i] - x[j]); } // n階差分商 double a[N]; //a[0] = d[0][0]; //a[1] = d[1][0]; //a[2] = d[2][0]; //a[3] = d[3][0]; //a[4] = d[4][0]; for (int j = 0; j < N; j++) a[j] = d[j][0]; // 0.05刻みで 与えられていない値を補間 for (int i = 0; i <= 20; i++) { double d = i * 0.05 - 0.5; double d1 = newton(d, x, a); double d2 = f(d); // 元の関数と比較 cout << setw(5) << fixed << setprecision(2) << d << ": "; cout << setw(8) << fixed << setprecision(5) << d1 << " - "; cout << setw(8) << fixed << setprecision(5) << d2 << " = "; cout << setw(8) << fixed << setprecision(5) << d1 - d2 << endl; } return 0; } // 元の関数 double f(double x) { return 4 * pow(x,4) + 3 * pow(x,3) - 2 * pow(x,2) - x + 1; } // Newton (ニュートン) 補間 double newton(double d, double x[], double a[]) { double sum = a[0]; //sum += a[1] * (d - x[0]); //sum += a[2] * (d - x[0]) * (d - x[1]); //sum += a[3] * (d - x[0]) * (d - x[1]) * (d - x[2]); //sum += a[4] * (d - x[0]) * (d - x[1]) * (d - x[2]) * (d - x[3]); for (int i = 1; i < N; i++) { double prod = 1; for (int j = 0; j < i; j++) prod *= (d - x[j]); sum += a[i] * prod; } return sum; }
Z:\>bcc32 CP0702.cpp Borland C++ 5.5.1 for Win32 Copyright (c) 1993, 2000 Borland cp0702.cpp: Turbo Incremental Link 5.00 Copyright (c) 1997, 2000 Borland Z:\>CP0702 -0.50: 0.87500 - 0.87500 = 0.00000 -0.45: 0.93565 - 0.93565 = -0.00000 -0.40: 0.99040 - 0.99040 = 0.00000 -0.35: 1.03640 - 1.03640 = 0.00000 -0.30: 1.07140 - 1.07140 = 0.00000 -0.25: 1.09375 - 1.09375 = 0.00000 -0.20: 1.10240 - 1.10240 = 0.00000 -0.15: 1.09690 - 1.09690 = 0.00000 -0.10: 1.07740 - 1.07740 = 0.00000 -0.05: 1.04465 - 1.04465 = 0.00000 0.00: 1.00000 - 1.00000 = 0.00000 0.05: 0.94540 - 0.94540 = -0.00000 0.10: 0.88340 - 0.88340 = 0.00000 0.15: 0.81715 - 0.81715 = 0.00000 0.20: 0.75040 - 0.75040 = 0.00000 0.25: 0.68750 - 0.68750 = 0.00000 0.30: 0.63340 - 0.63340 = -0.00000 0.35: 0.59365 - 0.59365 = -0.00000 0.40: 0.57440 - 0.57440 = 0.00000 0.45: 0.58240 - 0.58240 = 0.00000 0.50: 0.62500 - 0.62500 = 0.00000