C++ で連立一次方程式を解く(LU分解法)

連立一次方程式

を行列で表すと, こんな感じ

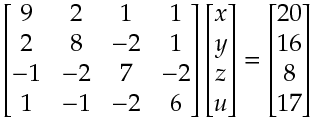
このとき

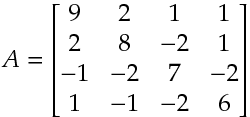
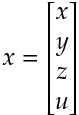
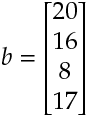
とすると, 最初の連立方程式は と表すことができる.

このとき となる 上三角行列 , 下三角行列 を考えると,

であり, とおくと となる.

LU分解法では, 係数行列 を上三角行列 , 下三角行列 に分解し,
から を求め, から を求める.

上三角行列 は, ガウスの消去法で使った上三角行列そのもので,当然求め方も同じ.
下三角行列 は, ガウスの消去法の計算途中で使った値を保存しておくだけ.
なので, ガウスの消去法とほとんど同じだが, 行列 の値だけを変えて繰り返し実行する場合に使う.

#include <iostream>
#include <iomanip>
#include <math.h>
using namespace std;

void decomp(double a[4][4], double b[4], double x[4]);

int main()
{
    double a[4][4] = {{-1,-2,7,-2},{1,-1,-2,6},{9,2,1,1},{2,8,-2,1}}; 
    double b[4]    = {8,17,20,16};
    double x[4]    = {0,0,0,0};

    decomp(a,b,x);
    for (int i = 0;i<=3;i++)
        cout << setw(12) << fixed << setprecision(10) << x[i] << "\t";
    cout << endl;
   
    return 0;
}

void decomp(double a[4][4], double b[4], double x[4])
{
    // ピボット選択
    int p[4] = {0,1,2,3};
    for(int pivot = 0; pivot < 4; pivot++)
    {
        // 各列で 一番値が大きい行を 探す
        int     col     =   pivot;
        int     max_row =   pivot;
        double  max_val =   0;
        for (int i = p[pivot]; i < 4; i++)
        {
            int row = p[i];
            if (fabs(a[row][col]) > max_val)
            {
                // 一番値が大きい行
                max_val =   fabs(a[row][col]);
                max_row =   row;
            }
        }

        // 一番値が大きい行と入れ替え
        if (max_row != p[pivot])
        {
            int tmp     =   p[pivot];
            p[pivot]    =   max_row;
            p[max_row]  =   tmp;
        }
    }
    
    // 並べ替え後の状態を確認
    for (int i = 0; i < 4; i++) 
    {
        for (int j = 0; j < 4; j++) 
            cout << setw(14) << fixed << setprecision(10) << a[p[i]][j] << "\t";
        cout << setw(14) << fixed << setprecision(10) << b[p[i]] << "\t";
        cout << endl;
    }
    cout << endl;

    // 前進消去
    for (int pivot = 0; pivot < 3; pivot++)
    {
        int p_row = p[pivot];
        int p_col = pivot;
        
        for (int i = pivot+1; i < 4; i++)
        {
            int     row = p[i];
            double  s   = a[row][p_col] / a[p_row][p_col];
            
            for (int col = pivot; col < 4; col++)
                a[row][col] -= a[p_row][col] * s; // これが 上三角行列
            a[row][p_col] = s;                    // これが 下三角行列
            // b[row]    -= b[p_row] * s;         // この値は変更しない
        }
    }
    // 前進消去後の状態を確認
    for (int i = 0; i < 4; i++) 
    {
        for (int j = 0; j < 4; j++) 
            cout << setw(14) << fixed << setprecision(10) << a[p[i]][j] << "\t";
        cout << setw(14) << fixed << setprecision(10) << b[p[i]] << "\t";
        cout << endl;
    }
    cout << endl;
    
    // Ly=b から y を求める
    double y[4] = {0,0,0,0};
    for (int i = 0; i < 4; i++)
    {
        int row = p[i];
        for (int col = 0; col < i; col++)
            b[row] -= a[row][col] * y[p[col]];
        y[row] = b[row];
    }
    // y の 値
    for (int i = 0;i<=3;i++)
        cout << setw(12) << fixed << setprecision(10) << y[p[i]] << "\t";
    cout << endl << endl;

    // Ux=y から x を求める
    for (int i = 3; i >= 0; i--)
    {
        int row = p[i];
        for (int col = 3; col >= i + 1; col--)
            y[row] -= a[row][col] * x[col];
        x[i] = y[row] / a[row][i];
    }
}

  9.0000000000	  2.0000000000	  1.0000000000	  1.0000000000	 20.0000000000	
  2.0000000000	  8.0000000000	 -2.0000000000	  1.0000000000	 16.0000000000	
 -1.0000000000	 -2.0000000000	  7.0000000000	 -2.0000000000	  8.0000000000	
  1.0000000000	 -1.0000000000	 -2.0000000000	  6.0000000000	 17.0000000000	

  9.0000000000	  2.0000000000	  1.0000000000	  1.0000000000	 20.0000000000	
  0.2222222222	  7.5555555556	 -2.2222222222	  0.7777777778	 16.0000000000	
 -0.1111111111	 -0.2352941176	  6.5882352941	 -1.7058823529	  8.0000000000	
  0.1111111111	 -0.1617647059	 -0.3750000000	  5.3750000000	 17.0000000000	

20.0000000000	11.5555555556	12.9411764706	21.5000000000	

1.0000000000	2.0000000000	3.0000000000	4.0000000000	

参考文献